看完上期分享的系列视频之后,自己也来动手做一个加法器。
这里使用的软件是logisim,一款比较老的模拟软件。
下面涉及到一些公式。⊕异或 · 与 +或 ⊙同或 ¬非
实现思路
单位加法(半加法器)
首先来看一下单位的加法,我们很容易就能得出下面的结论:
0+0=0
0+1=1
1+0=1
1+1=10
观察一下上面的四个二进制加法,找一找规律。
我们会发现每一个式子的结果的最后一位(称为本位 S)组合是0110,对照异或门的真值表我们会发现,单位加法的真值表与异或门的真值表完全一致。因此我们可以得出
本位S 的公式是 A⊕B = S
进位C 的公式是 A·B = C
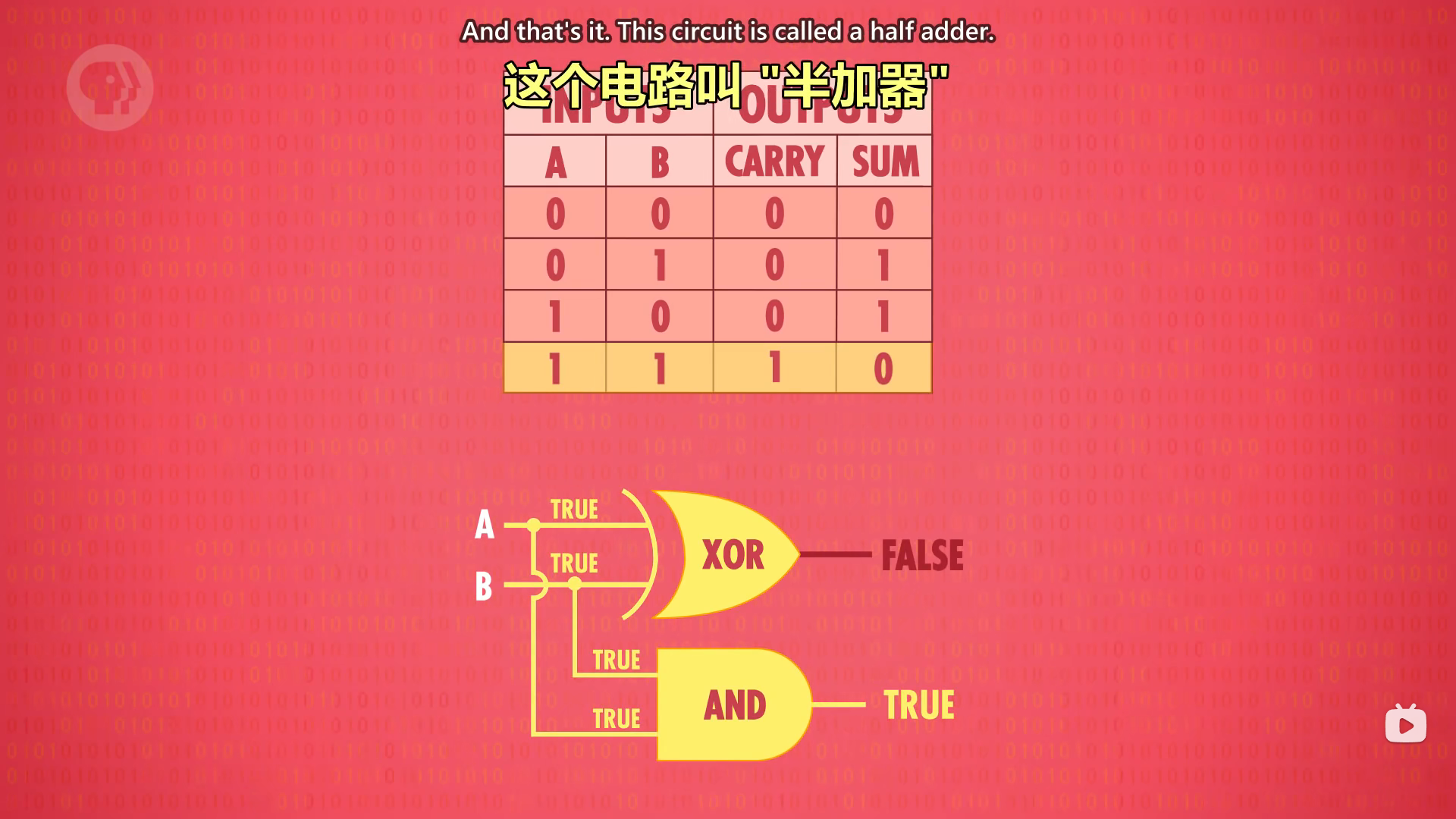
到这里我们就已经完成了一个半加法器,但是只能计算单位二进制。
这里我们将它们封装成一个一位的半加器,输入A、B并输出S、C。
三位数加法(全加器)
我们先来看一个三位数的加法:110(6)+010(2)=1000(8)
我们来试着用竖式计算一下:
先看最后一列(从右往左开始,下面的等号后面全部都是本位的结果,进位另外表示):
0+0=0 本位S0 = 0 进位C0 = 0
1+1 + 0 = 0 本位S1 = 0 进位 C1 = 1 (这里1+1后面继续加上了0,这个0来自上一行中的进位C0,也就是说,我们在进行多位加法的过程中,也要像十进制一样,计算完本列还要再加上上一位的进位才行)
1+0 +1 = 0 本位S = 0 进位C2 = 1 (这里又加上了上一位的进位C1 = 1,继续得到新的结果10)
计算到这里就已经结束了,我们发现,在进行每一列的运算时都要加上上一位输出的进位,因此我们就可以根据这样的运算规则,列出输入Ai、Bi、Ci输出S(out)、C(out)的真值表:
| A(input) | B(input) | C(input) | S(output) | C(output) |
| 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 | 0 |
| 0 | 1 | 0 | 1 | 0 |
| 0 | 1 | 1 | 0 | 1 |
| 1 | 0 | 0 | 1 | 0 |
| 1 | 0 | 1 | 0 | 1 |
| 1 | 1 | 0 | 0 | 1 |
| 1 | 1 | 1 | 1 | 1 |
由上表可以得出:
本位S的计算公式是 S=Ai⊕Bi⊕C
进位C的计算公式是 C=(Ai·Bi)+(Ai⊕Bi)
到这里你可能还不是很明白,还记得上面我们封装好的半加器吗?计算原理上面已经讲了,我们只需要将两个半加器串联在一起,把上一个半加器输出的本位输入到下一个半加器的输入A或B上,再将新的进位(与这两个半加器的输出进位不同)输入到下一个半加器,这样下一个半加器输出的S就是结果的本位。
那么我们要怎么得到结果进位呢?
很简单,只需要判断两个半加器的进位是否有任意一个是1,若是则结果进位为1,这也刚好符合或门的真值表。

这样我们就得到了一个全加器,图中的HALF ADDER就是我上面封装的半加器。
制作4位全加器
现在我们得到了全加器,现在又变得更简单了,只需要套用竖式的计算规则就能完成任意位数的加法器了。
首先根据上面全加器的原理制作一个全加器,逻辑电路如下:

现在根据计算规则将两个全加器串联在一起:
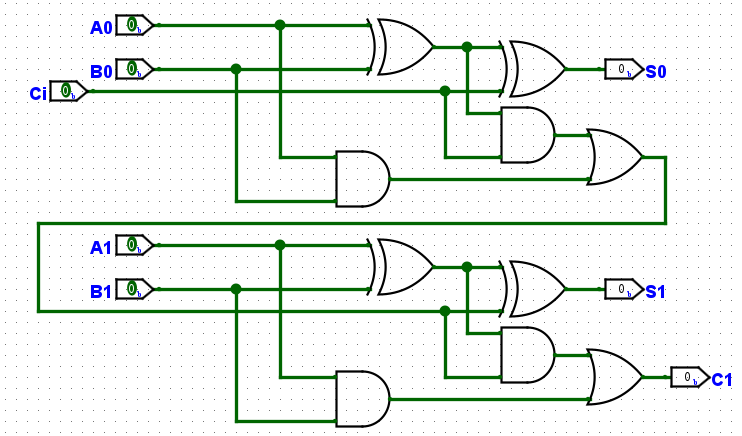
可以看到,原本上一位的进位现在已经输入到了下一位的输入进位上,这样我们就得到了一个2位的加法器。因此我们只需要再继续这样串联下去,就得到了N位加法器。
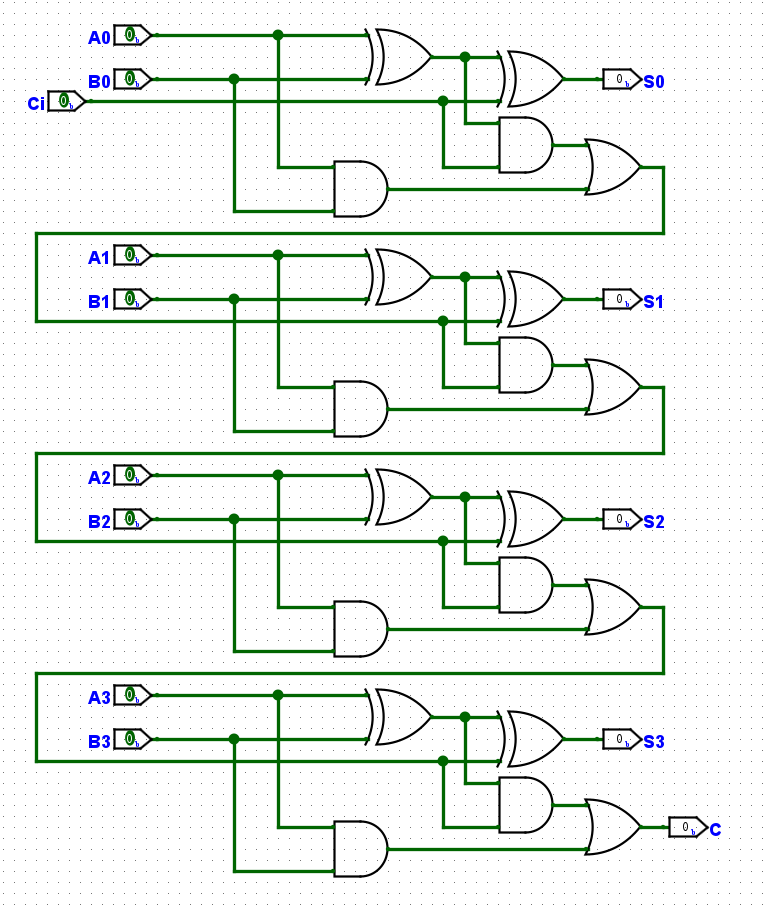
如上图所示,这就是一个四位的加法器,我们可以来验证一下上面的三位加法。
0110(6)+0010(2)=1000(8)
注意一下这里要倒序输入,意思就是:
A0输入0 A1输入1 A2输入1 A3输入0
B0输入0 B1输入1 B2输入0 B3输入0

我们倒着看结果,得到01000(8)。
到这里就已经完成一个4位的加法器,但我们得到了五位数,这个五位数的第一位称为溢出位。
例如当我们计算1111+0001时,结果是10000,很显然得到的结果无法用4位表示,因此就超过4位溢出了,但我们可以得到溢出位从而完整的表示4位数加法的结果。




